Random Notes
LLN and CLT
- Law of Large Number: \[
\text{For any small }\epsilon>0,
Pr(\mid\frac{L_1+L_2+...+L_N}{N}-\mu<\epsilon\mid)\rightarrow1 \text{
as } N\rightarrow \infty \]
- where \(L_i\) can be loss of person \(i\) and all \(L_i\) has mean \(\mu\).
- This means when sample size is big enough, sample mean will approach the true mean.
- LLN is useful when thinking about the more people are insured, the actual average loss is close to the true loss.
- Central Limit Theorm: \[
\text{Regardless of how } L_i \text{ distributes, }
\frac{L_1+L_2+...+L_N}{N}\rightarrow Normal (\mu,\sigma/\sqrt{N}) \text{
as } N\rightarrow \infty.\]
- This means the random variable, sample mean, will become very close to normal and get narrower if sample size is big enough.
- CLT is useful when thinking about calculating incident (mortality) rate. e.g. The more people are observed for survival(0) or death(1) in 70 years old, (\(L_i\in\{0,1\}\)), then \(\frac{L_1+L_2+...+L_N}{N}=D/N\) if \(D\) is the number of deaths. If \(N\) is big enought, then this probability estimation will be close to normally distributed, with a mean close to the true \(p\) and a standard deviation \(\sigma/\sqrt{N}\).
Estimation properties
- Small (finite) sample property – apply to all sample sizes (small
and large)
- Bias
- An estimator is unbiased if, on average, it hits the true parameter value. That is, the mean of the sampling distribution of the estimator is equal to the true parameter value.
- Throw darts to an x-y plane, guessing the how “accurate” to throw it at center \(\Rightarrow\) expected value is (0,0) because postive and negative cancel eath other \[E(W)=\theta \Leftrightarrow W\text{ is an unbiased estimator of }\theta\]
- Efficiency
- Given two unbiased estimators of \(\theta\), an estimator \(W_1\) is efficient relative to \(W_2\) if \(Var(W1)\leq Var(W2) \quad \forall \theta\)
- Bias
- Large sample (asymptotic) property
- Consistency
- An estimator is consistent if, as the sample size increases, the estimates (produced by the estimator) “converge” to the true value of the parameter being estimated. To be slightly more precise - consistency means that, as the sample size increases, the sampling distribution of the estimator becomes increasingly concentrated at the true parameter value.
- As sample size \(n\rightarrow \infty\), \(P(\mid W_n-\theta\mid>\epsilon)\rightarrow 0\)
- Consistency
Unbiasedness and consistency are not equivalent: Unbiasedness is a statement about the expected value of the sampling distribution of the estimator. Consistency is a statement about “where the sampling distribution of the estimator is going” as the sample size increases.
Generalized least square
- GLS \(\rightarrow\) WLS (a special case of)
- To solve heteroskadastisity (so does robust s.e.)
\[\Sigma = \begin{bmatrix} {1}/{\sigma^2_1} & 0 & 0 & \ldots & 0\\ 0 & {1}/{\sigma^2_2} & 0 & \ldots & 0\\ 0 & 0 & {1}/{\sigma^2_3} & \ldots & 0\\ 0 & 0 & 0 & \ldots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & \ldots & 1/\sigma^2_n \end{bmatrix}\rightarrow \boxed{\text{Weighted by } \frac{1}{\sigma^2_i}} \]
Generalized method of moments
- It is used to estimate IV
- # of parameters < # of moment conditions e.g.
\[ \begin{split} &\Rightarrow\frac{1}{N}\sum x_i=\hat{\mu} \quad &\boxed{\text{Equality}} \\ &\Rightarrow g_1 = \frac{1}{N}\sum x_i -\hat{\mu} \quad&\boxed{\text{Miniize difference}} \end{split} \]
Fixed Effect & Clustering
Two ways of getting fixed effect estimation and clustering standard
errors: plm and felm. They are consistent
without fixed effect, and are slightly different in degree of freedom
adjustment when running with either one or both dimensions of fixed
effect.
When both a firm and a time effect are present in the data, researchers can address one parametrically (e.g., by including time dummies) and then estimate standard errors clustered on the other dimension. Alternatively, researchers can cluster on multiple dimensions. When there are a sufficient number of clusters in each dimension, standard errors clustered on multiple dimensions are unbiased and produce correctly sized confidence intervals whether the firm effect is permanent or temporary. ~ Petersen (2008)
# Loading the required libraries
library(plm)
library(lmtest)
library(multiwayvcov)
library(lfe)
library(stargazer)
# Loading Petersen's dataset
data(petersen)
# Pooled OLS model
pooled.ols<-plm(y~x,data=petersen,model="pooling",index=c("firmid", "year"))
# Fixed effects model
fe.firm<-plm(y~x,data=petersen,model="within",index=c("firmid", "year"))# Clustered standard errors - OLS (by firm)
m1 = coeftest(pooled.ols,vcov=vcovHC(pooled.ols,type="sss",cluster="group"))
m2 = felm(y~x|0|0|firmid,data=petersen)
stargazer(m1,m2,type='html')##
## <table style="text-align:center"><tr><td colspan="3" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"></td><td colspan="2"><em>Dependent variable:</em></td></tr>
## <tr><td></td><td colspan="2" style="border-bottom: 1px solid black"></td></tr>
## <tr><td style="text-align:left"></td><td></td><td>y</td></tr>
## <tr><td style="text-align:left"></td><td><em>coefficient</em></td><td><em>felm</em></td></tr>
## <tr><td style="text-align:left"></td><td><em>test</em></td><td><em></em></td></tr>
## <tr><td style="text-align:left"></td><td>(1)</td><td>(2)</td></tr>
## <tr><td colspan="3" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">x</td><td>1.035<sup>***</sup></td><td>1.035<sup>***</sup></td></tr>
## <tr><td style="text-align:left"></td><td>(0.051)</td><td>(0.051)</td></tr>
## <tr><td style="text-align:left"></td><td></td><td></td></tr>
## <tr><td style="text-align:left">Constant</td><td>0.030</td><td>0.030</td></tr>
## <tr><td style="text-align:left"></td><td>(0.067)</td><td>(0.067)</td></tr>
## <tr><td style="text-align:left"></td><td></td><td></td></tr>
## <tr><td colspan="3" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Observations</td><td></td><td>5,000</td></tr>
## <tr><td style="text-align:left">R<sup>2</sup></td><td></td><td>0.208</td></tr>
## <tr><td style="text-align:left">Adjusted R<sup>2</sup></td><td></td><td>0.208</td></tr>
## <tr><td style="text-align:left">Residual Std. Error</td><td></td><td>2.005 (df = 4998)</td></tr>
## <tr><td colspan="3" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"><em>Note:</em></td><td colspan="2" style="text-align:right"><sup>*</sup>p<0.1; <sup>**</sup>p<0.05; <sup>***</sup>p<0.01</td></tr>
## </table># Clustered standard errors - OLS (by time)
m1 = coeftest(pooled.ols,vcov=vcovHC(pooled.ols,type="sss",cluster="time"))
m2 = felm(y~x|0|0|year,data=petersen)
stargazer(m1,m2,type='html')##
## <table style="text-align:center"><tr><td colspan="3" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"></td><td colspan="2"><em>Dependent variable:</em></td></tr>
## <tr><td></td><td colspan="2" style="border-bottom: 1px solid black"></td></tr>
## <tr><td style="text-align:left"></td><td></td><td>y</td></tr>
## <tr><td style="text-align:left"></td><td><em>coefficient</em></td><td><em>felm</em></td></tr>
## <tr><td style="text-align:left"></td><td><em>test</em></td><td><em></em></td></tr>
## <tr><td style="text-align:left"></td><td>(1)</td><td>(2)</td></tr>
## <tr><td colspan="3" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">x</td><td>1.035<sup>***</sup></td><td>1.035<sup>***</sup></td></tr>
## <tr><td style="text-align:left"></td><td>(0.033)</td><td>(0.033)</td></tr>
## <tr><td style="text-align:left"></td><td></td><td></td></tr>
## <tr><td style="text-align:left">Constant</td><td>0.030</td><td>0.030</td></tr>
## <tr><td style="text-align:left"></td><td>(0.023)</td><td>(0.023)</td></tr>
## <tr><td style="text-align:left"></td><td></td><td></td></tr>
## <tr><td colspan="3" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Observations</td><td></td><td>5,000</td></tr>
## <tr><td style="text-align:left">R<sup>2</sup></td><td></td><td>0.208</td></tr>
## <tr><td style="text-align:left">Adjusted R<sup>2</sup></td><td></td><td>0.208</td></tr>
## <tr><td style="text-align:left">Residual Std. Error</td><td></td><td>2.005 (df = 4998)</td></tr>
## <tr><td colspan="3" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"><em>Note:</em></td><td colspan="2" style="text-align:right"><sup>*</sup>p<0.1; <sup>**</sup>p<0.05; <sup>***</sup>p<0.01</td></tr>
## </table># Clustered standard errors - OLS (by firm and time)
m1 = coeftest(pooled.ols,vcov=vcovDC(pooled.ols,type="sss"))
m2 = felm(y~x|0|0|firmid+year,data=petersen)
stargazer(m1,m2,type='html')##
## <table style="text-align:center"><tr><td colspan="3" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"></td><td colspan="2"><em>Dependent variable:</em></td></tr>
## <tr><td></td><td colspan="2" style="border-bottom: 1px solid black"></td></tr>
## <tr><td style="text-align:left"></td><td></td><td>y</td></tr>
## <tr><td style="text-align:left"></td><td><em>coefficient</em></td><td><em>felm</em></td></tr>
## <tr><td style="text-align:left"></td><td><em>test</em></td><td><em></em></td></tr>
## <tr><td style="text-align:left"></td><td>(1)</td><td>(2)</td></tr>
## <tr><td colspan="3" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">x</td><td>1.035<sup>***</sup></td><td>1.035<sup>***</sup></td></tr>
## <tr><td style="text-align:left"></td><td>(0.054)</td><td>(0.054)</td></tr>
## <tr><td style="text-align:left"></td><td></td><td></td></tr>
## <tr><td style="text-align:left">Constant</td><td>0.030</td><td>0.030</td></tr>
## <tr><td style="text-align:left"></td><td>(0.065)</td><td>(0.065)</td></tr>
## <tr><td style="text-align:left"></td><td></td><td></td></tr>
## <tr><td colspan="3" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Observations</td><td></td><td>5,000</td></tr>
## <tr><td style="text-align:left">R<sup>2</sup></td><td></td><td>0.208</td></tr>
## <tr><td style="text-align:left">Adjusted R<sup>2</sup></td><td></td><td>0.208</td></tr>
## <tr><td style="text-align:left">Residual Std. Error</td><td></td><td>2.005 (df = 4998)</td></tr>
## <tr><td colspan="3" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"><em>Note:</em></td><td colspan="2" style="text-align:right"><sup>*</sup>p<0.1; <sup>**</sup>p<0.05; <sup>***</sup>p<0.01</td></tr>
## </table># Clustered standard errors - Fixed effect regression (by firm)
m1 = coeftest(fe.firm,vcov=vcovHC(fe.firm,type="sss",cluster="group"))
m2 = felm(y~x|firmid|0|firmid,data=petersen)
stargazer(m1,m2,type='html')##
## <table style="text-align:center"><tr><td colspan="3" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"></td><td colspan="2"><em>Dependent variable:</em></td></tr>
## <tr><td></td><td colspan="2" style="border-bottom: 1px solid black"></td></tr>
## <tr><td style="text-align:left"></td><td></td><td>y</td></tr>
## <tr><td style="text-align:left"></td><td><em>coefficient</em></td><td><em>felm</em></td></tr>
## <tr><td style="text-align:left"></td><td><em>test</em></td><td><em></em></td></tr>
## <tr><td style="text-align:left"></td><td>(1)</td><td>(2)</td></tr>
## <tr><td colspan="3" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">x</td><td>0.970<sup>***</sup></td><td>0.970<sup>***</sup></td></tr>
## <tr><td style="text-align:left"></td><td>(0.030)</td><td>(0.030)</td></tr>
## <tr><td style="text-align:left"></td><td></td><td></td></tr>
## <tr><td colspan="3" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Observations</td><td></td><td>5,000</td></tr>
## <tr><td style="text-align:left">R<sup>2</sup></td><td></td><td>0.650</td></tr>
## <tr><td style="text-align:left">Adjusted R<sup>2</sup></td><td></td><td>0.611</td></tr>
## <tr><td style="text-align:left">Residual Std. Error</td><td></td><td>1.406 (df = 4499)</td></tr>
## <tr><td colspan="3" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"><em>Note:</em></td><td colspan="2" style="text-align:right"><sup>*</sup>p<0.1; <sup>**</sup>p<0.05; <sup>***</sup>p<0.01</td></tr>
## </table># Clustered standard errors - Fixed effect regression (by time)
m1 = coeftest(fe.firm,vcov=vcovHC(fe.firm,type="sss",cluster="time"))
m2 = felm(y~x|firmid|0|year,data=petersen)
stargazer(m1,m2,type='html')##
## <table style="text-align:center"><tr><td colspan="3" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"></td><td colspan="2"><em>Dependent variable:</em></td></tr>
## <tr><td></td><td colspan="2" style="border-bottom: 1px solid black"></td></tr>
## <tr><td style="text-align:left"></td><td></td><td>y</td></tr>
## <tr><td style="text-align:left"></td><td><em>coefficient</em></td><td><em>felm</em></td></tr>
## <tr><td style="text-align:left"></td><td><em>test</em></td><td><em></em></td></tr>
## <tr><td style="text-align:left"></td><td>(1)</td><td>(2)</td></tr>
## <tr><td colspan="3" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">x</td><td>0.970<sup>***</sup></td><td>0.970<sup>***</sup></td></tr>
## <tr><td style="text-align:left"></td><td>(0.027)</td><td>(0.028)</td></tr>
## <tr><td style="text-align:left"></td><td></td><td></td></tr>
## <tr><td colspan="3" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Observations</td><td></td><td>5,000</td></tr>
## <tr><td style="text-align:left">R<sup>2</sup></td><td></td><td>0.650</td></tr>
## <tr><td style="text-align:left">Adjusted R<sup>2</sup></td><td></td><td>0.611</td></tr>
## <tr><td style="text-align:left">Residual Std. Error</td><td></td><td>1.406 (df = 4499)</td></tr>
## <tr><td colspan="3" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"><em>Note:</em></td><td colspan="2" style="text-align:right"><sup>*</sup>p<0.1; <sup>**</sup>p<0.05; <sup>***</sup>p<0.01</td></tr>
## </table># Clustered standard errors - Fixed effect regression (by firm and time)
m1 = coeftest(fe.firm,vcov=vcovDC(fe.firm,type="sss"))
m2 = felm(y~x|firmid|0|firmid+year,data=petersen)
stargazer(m1,m2,type='html')##
## <table style="text-align:center"><tr><td colspan="3" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"></td><td colspan="2"><em>Dependent variable:</em></td></tr>
## <tr><td></td><td colspan="2" style="border-bottom: 1px solid black"></td></tr>
## <tr><td style="text-align:left"></td><td></td><td>y</td></tr>
## <tr><td style="text-align:left"></td><td><em>coefficient</em></td><td><em>felm</em></td></tr>
## <tr><td style="text-align:left"></td><td><em>test</em></td><td><em></em></td></tr>
## <tr><td style="text-align:left"></td><td>(1)</td><td>(2)</td></tr>
## <tr><td colspan="3" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">x</td><td>0.970<sup>***</sup></td><td>0.970<sup>***</sup></td></tr>
## <tr><td style="text-align:left"></td><td>(0.029)</td><td>(0.029)</td></tr>
## <tr><td style="text-align:left"></td><td></td><td></td></tr>
## <tr><td colspan="3" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Observations</td><td></td><td>5,000</td></tr>
## <tr><td style="text-align:left">R<sup>2</sup></td><td></td><td>0.650</td></tr>
## <tr><td style="text-align:left">Adjusted R<sup>2</sup></td><td></td><td>0.611</td></tr>
## <tr><td style="text-align:left">Residual Std. Error</td><td></td><td>1.406 (df = 4499)</td></tr>
## <tr><td colspan="3" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"><em>Note:</em></td><td colspan="2" style="text-align:right"><sup>*</sup>p<0.1; <sup>**</sup>p<0.05; <sup>***</sup>p<0.01</td></tr>
## </table>Debugging
- Function to trace back to upper level:
recover().
R Markdown Note
- Link:
[link](http://xxxx.com) - Quote:
>abc - Numbered header
#. - Stargazer header removal:
header=FALSE - Upload website to github:
- Build Website
- Command in shell
git add -Agit commit -m "My first website"git push origin master
- Matrices
- Jacobian
- Change of variable
x,y\(\to\)u,v - Determinant of \[\left[\begin{array}{rr}\frac{dx}{du} & \frac{dx}{dv}\\ \frac{dy}{du} & \frac{dy}{dv}\end{array}\right] \]
- Change of variable
- Hessian: all combinations of 2nd derivative
- Jacobian
- Output word file –
kableExtrashould be taken out. It messes with table formatting. - Dealing with pdflatex.exe
Sorry, but C:\Users\xxx\AppData\Local\Programs\MIKTEX~1.9\miktex\bin\x64\pdflatex.exe did not succeed- Keep tex file
- Compile tex
- Install (update) whatever is necessary
- Update R & rstudio
- Windows: installr::updateR()
- MacOS: https://cloud.r-project.org/bin/macosx/
Relevel Factor
- Change reference group to:
relevel(RATING,4)
A List of Regressions
Applying the regression function on a list of data gives a flexibility and convenience to run hundreds of regression models just with 3~4 lines of code.
The following performs year fixed effect regression with firm
clustering on a set of varing dependent variables (2) and independent
variables (11). lapply applies the regression funciton to
each rating change, and for loop changes the dependent variable through
NONGRP_AVE and TOTAL_AVE. Differences in the
dependent variables are recorded in the first dimesion of the list
[[i]] whereas the differences of independent variables are
recorded in the second dimension [[i]][[1:11]]. Results are
presented by stargazer package.
my_dep<-c("NONGRP_AVE","TOTAL_AVE")
my_lm <-list(1:2)
#--------------------------------------------------------------------------
for(i in 1:2){
my_lm[[i]]<-lapply(1:10, function(x) felm(get(my_dep[i]) ~ I(RATING>x)
+SINGLE+HERF+NATIONAL+NYREG+STOCK+SIZE+AGE+lag(REINS)|YEAR|0|COCODE,data=MainData))
test<-felm(get(my_dep[i]) ~ RATING
+SINGLE+HERF+NATIONAL+NYREG+STOCK+SIZE+AGE+lag(REINS)|YEAR|0|COCODE,data=MainData)
my_lm[[i]][[11]]<-test
}stargazer::stargazer(my_lm[1],type='html',dep.var.labels=my_dep[1])| Dependent variable: | |||||||||||
| NONGRP | |||||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | |
| I(RATING > x) | -97.697*** | -79.936*** | -67.244*** | -33.182*** | -15.331** | -7.238 | -4.379 | 2.816 | 7.817 | -1.826 | |
| (26.442) | (11.482) | (8.280) | (7.097) | (6.584) | (5.693) | (6.496) | (7.269) | (8.283) | (10.305) | ||
| RATING | -12.762*** | ||||||||||
| (1.849) | |||||||||||
| SINGLE | -5.737 | 0.173 | 7.253 | 1.143 | -4.010 | -6.445 | -6.988 | -7.427 | -7.583 | -7.237 | 6.889 |
| (7.753) | (7.470) | (7.308) | (7.521) | (7.732) | (7.842) | (7.861) | (7.860) | (7.865) | (7.872) | (7.588) | |
| HERF | 37.456 | 56.087* | 68.402** | 46.180 | 37.625 | 34.789 | 34.429 | 32.847 | 32.175 | 33.613 | 65.319* |
| (34.524) | (34.040) | (34.534) | (34.592) | (34.884) | (34.885) | (34.923) | (34.973) | (34.917) | (34.868) | (35.197) | |
| NATIONAL | 17.129 | 21.939* | 20.638* | 17.185 | 16.513 | 16.736 | 16.660 | 16.845 | 16.814 | 16.784 | 17.462 |
| (12.557) | (12.191) | (12.453) | (12.713) | (12.759) | (12.775) | (12.787) | (12.782) | (12.778) | (12.780) | (12.524) | |
| NYREG | 37.970*** | 34.696*** | 32.860** | 38.385*** | 41.189*** | 42.375*** | 42.619*** | 42.805*** | 42.837*** | 42.740*** | 34.538** |
| (13.497) | (13.223) | (13.400) | (13.825) | (13.912) | (13.906) | (13.896) | (13.897) | (13.894) | (13.891) | (13.538) | |
| STOCK | -5.713 | -11.172 | -8.333 | -2.953 | -4.709 | -5.567 | -5.770 | -5.994 | -6.206 | -5.869 | -2.696 |
| (15.488) | (15.342) | (15.627) | (15.968) | (16.021) | (16.045) | (16.045) | (16.052) | (16.081) | (16.054) | (15.660) | |
| SIZE | 22.659*** | 16.580*** | 16.615*** | 21.565*** | 23.991*** | 24.994*** | 25.217*** | 25.356*** | 25.414*** | 25.303*** | 18.038*** |
| (2.576) | (2.613) | (2.907) | (3.116) | (3.040) | (2.890) | (2.826) | (2.813) | (2.816) | (2.795) | (2.953) | |
| AGE | -0.083 | -0.032 | -0.025 | -0.061 | -0.094 | -0.110 | -0.113 | -0.117 | -0.119 | -0.115 | -0.007 |
| (0.153) | (0.150) | (0.151) | (0.155) | (0.157) | (0.158) | (0.159) | (0.159) | (0.159) | (0.158) | (0.151) | |
| lag(REINS) | 38.098** | 35.487** | 36.259** | 35.282** | 35.820** | 35.069** | 35.119** | 35.198** | 35.277** | 35.165** | 35.995** |
| (15.809) | (15.296) | (15.506) | (15.774) | (15.847) | (15.872) | (15.875) | (15.883) | (15.894) | (15.876) | (15.616) | |
| Observations | 13,493 | 13,493 | 13,493 | 13,493 | 13,493 | 13,493 | 13,493 | 13,493 | 13,493 | 13,493 | 13,493 |
| R2 | 0.186 | 0.202 | 0.194 | 0.175 | 0.171 | 0.170 | 0.170 | 0.170 | 0.170 | 0.170 | 0.185 |
| Adjusted R2 | 0.184 | 0.201 | 0.192 | 0.173 | 0.169 | 0.168 | 0.168 | 0.168 | 0.168 | 0.168 | 0.183 |
| Residual Std. Error (df = 13459) | 151.741 | 150.219 | 151.061 | 152.749 | 153.132 | 153.214 | 153.225 | 153.227 | 153.223 | 153.228 | 151.841 |
| Note: | p<0.1; p<0.05; p<0.01 | ||||||||||
stargazer::stargazer(my_lm[2],type='html',dep.var.labels=my_dep[2])| Dependent variable: | |||||||||||
| TOTAL | |||||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | |
| I(RATING > x) | -130.653 | 46.351 | -160.637 | -437.823*** | -254.502** | -230.231*** | -271.076*** | -243.274*** | -262.390*** | -292.255*** | |
| (244.521) | (127.130) | (119.996) | (122.237) | (103.829) | (79.973) | (85.210) | (91.532) | (94.030) | (104.040) | ||
| RATING | -65.049*** | ||||||||||
| (25.076) | |||||||||||
| SINGLE | 55.107 | 48.729 | 87.758 | 164.143 | 107.276 | 79.488 | 70.912 | 66.062 | 63.340 | 59.371 | 125.252 |
| (123.888) | (124.025) | (126.355) | (121.644) | (120.891) | (124.972) | (125.521) | (125.480) | (125.224) | (124.819) | (123.372) | |
| HERF | -35.390 | -53.910 | 42.768 | 127.440 | 28.853 | 2.436 | 21.000 | 9.651 | 1.381 | -11.628 | 121.763 |
| (482.940) | (473.098) | (488.152) | (491.043) | (490.149) | (488.438) | (489.740) | (489.904) | (489.091) | (487.293) | (488.616) | |
| NATIONAL | 360.713** | 357.265** | 369.458** | 365.529** | 355.735** | 358.704** | 352.500** | 355.095** | 359.290** | 360.089** | 363.702** |
| (152.168) | (152.774) | (153.526) | (151.708) | (151.925) | (152.213) | (151.856) | (151.967) | (152.247) | (152.299) | (152.038) | |
| NYREG | 611.539*** | 622.600*** | 594.305*** | 560.352*** | 592.041*** | 606.035*** | 609.880*** | 613.123*** | 614.970*** | 616.519*** | 576.080*** |
| (176.824) | (175.978) | (174.258) | (172.602) | (174.346) | (175.061) | (175.531) | (175.717) | (175.896) | (176.031) | (173.261) | |
| STOCK | 436.359*** | 439.154*** | 430.303*** | 475.070*** | 455.974*** | 446.890*** | 444.556*** | 443.710*** | 446.165*** | 442.091*** | 452.466*** |
| (136.306) | (139.835) | (135.493) | (136.969) | (136.165) | (136.509) | (136.644) | (136.808) | (136.928) | (136.459) | (135.493) | |
| SIZE | -5.512 | 3.107 | -22.745 | -51.448 | -23.946 | -12.206 | -8.069 | -5.455 | -5.255 | -4.102 | -39.053 |
| (29.898) | (33.784) | (35.889) | (35.719) | (32.787) | (29.991) | (28.998) | (28.625) | (28.588) | (28.273) | (37.343) | |
| AGE | 0.147 | 0.055 | 0.319 | 0.820 | 0.465 | 0.288 | 0.277 | 0.223 | 0.216 | 0.166 | 0.658 |
| (1.752) | (1.706) | (1.763) | (1.754) | (1.756) | (1.763) | (1.767) | (1.768) | (1.770) | (1.767) | (1.735) | |
| lag(REINS) | -120.597 | -124.700 | -121.909 | -123.014 | -113.706 | -127.694 | -127.550 | -127.077 | -128.148 | -125.100 | -120.301 |
| (154.283) | (154.138) | (154.464) | (154.300) | (154.676) | (154.227) | (154.145) | (154.190) | (154.173) | (154.110) | (154.654) | |
| Observations | 13,493 | 13,493 | 13,493 | 13,493 | 13,493 | 13,493 | 13,493 | 13,493 | 13,493 | 13,493 | 13,493 |
| R2 | 0.029 | 0.029 | 0.030 | 0.035 | 0.031 | 0.030 | 0.030 | 0.029 | 0.029 | 0.029 | 0.032 |
| Adjusted R2 | 0.027 | 0.026 | 0.027 | 0.033 | 0.028 | 0.027 | 0.027 | 0.027 | 0.027 | 0.027 | 0.029 |
| Residual Std. Error (df = 13459) | 1,947.611 | 1,947.741 | 1,946.853 | 1,941.258 | 1,945.739 | 1,946.677 | 1,946.925 | 1,947.343 | 1,947.397 | 1,947.496 | 1,944.996 |
| Note: | p<0.1; p<0.05; p<0.01 | ||||||||||
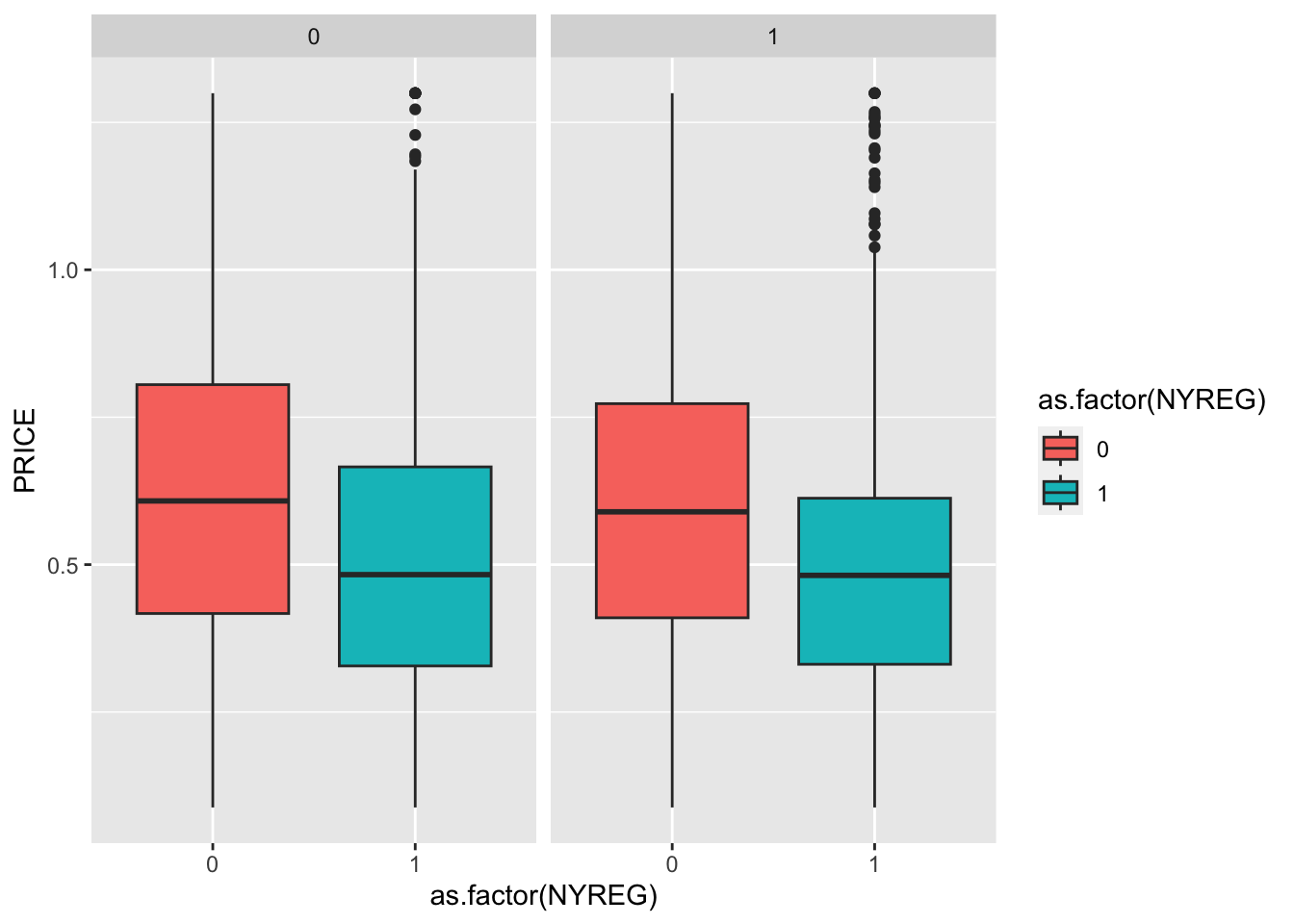
Multiple Boxplot
library(tableone)
CreateTableOne(data=MainData[MainData$PRE==0,],vars='PRICE',strata = 'NYREG')## Stratified by NYREG
## 0 1 p test
## n 2679 760
## PRICE (mean (SD)) 0.62 (0.27) 0.52 (0.26) <0.001CreateTableOne(data=MainData[MainData$PRE==1,],vars='PRICE',strata = 'NYREG')## Stratified by NYREG
## 0 1 p test
## n 6384 1871
## PRICE (mean (SD)) 0.60 (0.25) 0.49 (0.22) <0.001ggplot(MainData, aes(x=as.factor(NYREG),y=PRICE,fill=as.factor(NYREG))) + geom_boxplot()+facet_wrap(~PRE)